Even though I’ve been playing Kerbal Space Program for over a year, I have only barely explored the outer kerbolar system. I have been around Jool before and I have even landed on Laythe but never managed to make a round trip until this week.
Traveling all the way to Jool’s moon Laythe and back is not easy[citation needed]. It’s not so much getting there—although that’s not trivial, either—but we want to land on Laythe and we want to get back to orbit later: that takes a lot of fuel.
This is my adventure.
Mission Overview
The Kerbal Air and Space Agency (KASA) will be sending two separate missions: the Laythe Recovery System (LARS) and the Laythe Orbital Landing System (LOLS). The LARS stack is controlled by an automated probe and its function is to carry fuel for the travel back.

Although huge, it is only as heavy as it needs to be to deliver fuel, lacking scientific instrumentation and communication systems other than the Clamp-O-Tron’s acquisition signal.
The second stack is LOLS, which will carry a 3-kerbal crew, the lander itself, and all the scientific instruments: a gravioli detector, a termometer, a barometer, and a Mystery Goo™.
The two stacks will launch a couple of days between them and will meet in orbit around Jool over two years later. LOLS will then rendezvous with LARS, dock, and transfer any remaining fuel from its tanks and then drop its large tank before the LARS will then make the Hoffman transfer to Laythe1.
LARS Launch and Trans-joolian Insertion Burn
The first of the two missions to launch was LARS, the rationale being that if something were to go wrong later that prevented the LOLS launch, LARS could wait in Jool orbit for the several years until a new interplanetary window opened to allow LOLS—or its successor—to go rendezvous with it. It would be harder to keep a Kerbal crew waiting there2.
Also, to minimze the risks, LARS was launched as soon as the window opened, allowing for more time to deal with any issues with LOLS later. This resulted in a night launch.

Showing that LARS was not too heavy, it quickly started accelerating towards terminal velocity and we lower the thrust to about 80% so we don’t waste fuel fighting drag.

At 7300m we start the roll program to begin gaining horizontal speed. A little later, just passing the 10,000m mark our two first boosters run dry and we have a beautiful separation.

At its parking altitude of 240Km, the probe circularizes its orbit and, as Robert Heinlein would have said it, we are halfway to anywhere3.

About 2 hours after settling in its parking orbit, LARS is GO for TJI. This burn adds the 1,907m/s delta-V needed for LARS to reach Jool.

After the burn is done, LARS is on its way. Time to remember to extend our four Gigantor solar panels to ensure the probe will have power in its journey4.

With LARS now on the way, the KSP staff turns its attention to their next mission: LOLS.
LOLS Launch and Trans-joolian Insertion Burn
LOLS presents its own set of challenges. It is considerably heavier than LARS because not only it carries a similar amount of fuel—which it will spend much more quickly due to the extra mass—but it also adds the crew, large capsule, and scientific instrumentation.
With the greater weight, the engines struggle to lift off the launch pad. It takes almost 20 seconds to clear the flag pole by the pad.

It never comes close to terminal velocity while in the atmosphere and the throttle remains at 100% all the way. It begins roll program at 7300m and has barely accelerated past the 200m/s mark at this point.

After another beautiful separation, the speed is mounting a bit faster now…

… but it still takes a while. As well, although LARS managed to reach orbit on its second stage alone–albeit running on fumes at the end—, LOLS had to rely on the third stage to reach orbit, spending half its fuel tank.

About 90 minutes after reaching the parking orbit, LOLS is GO for TJI. Delta-V needed is 1,904m/s.

Over a million kilometers behind LARS, LOLS is now on its way for the long, nearly-two-year-long journey to Jool.
Deep space Transfer
During the long transfer period spend after escaping Kerbin’s sphere of influence and before the encouter with Jool, the crew does some science.

Tonmen Kerman goes EVA for a while and reports back to Kerbin. They also do a crew report and use the gravioli detector for some extra science production.
The original plan was to have LARS arriving first and waiting for LOLS to arrive. That would make sense as LARS is an automated probe while LOLS is carrying actual kerbals. That is why mission control5 naïvely launched LARS first. As it turns out, it was a mistake.

As you can see in this picture, LARS is indeed ahead of LOLS. However, due to their positions in relation to Jool itself, LOLS ends up getting caught by the Jool sphere of influence before LARS. This caught mission control by surprise and almost ended the mission as all its attention was on the LARS approach and only by sheer dumb luck they noticed LOLS encountering Jool SOI.

In retrospect, this makes perfect sense. In the 1-2 days following the launch of LARS, Kerbin and Jool were moving in relation with each other. Kerbin, having a much lower orbit than Jool’s, was moving faster and since it was “behind” Jool, this meant both planets were actually getting closer to each other so LOLS had a slightly shorter trip than LARS. That’s orbital mechanics for you.
LOLS Aerobreaking and Joolian Orbit Insertion Burn
One year, 270 days into the mission, LOLS, already deep inside the joolian SOI, maneuvered to adjust its periapsis to 110Km above Jool. Jool’s atmosphere begins at around 138Km of its sea level, which is not that much considering how big the planet is. But that atmosphere is very dense, which is good for aerobreaking, saving us some precious fuel.

Two days later, LOLS reaches Jool…

… and falls 30Km into its dense atmosphere for some heartstopping aerobreaking.

Mission control found 105Km to be a great aerobreaking altitude as LOLS re-emerged from the atmosphere with an apoapsis of a tad over 500Km, which required very little delta-V during the Joolian Orbit Insertion burn to reach the desired parking orbit of 400Km. The crew adjusted their apoapsis and periapsis and waited for the LARS to arrive. This was the early hours of 1y 273d MET6.
LARS Aerobreaking and Joolian Orbit Insertion Burn
Twenty seven days after the arrival of LOLS in Jool, LARS enters Jool’s SOI. LARS will try for an approach with a periapsis a little lower: 105Km. The 5Km difference doesn’t sound much but considering the density of Jool’s atmosphere, it makes a difference.
Despite mission control’s best efforts to point it retrograde, LARS insisted in going nose first.

LARS leaves the atmosphere with a apoapsis of a little under 400Km, again leaving little delta-V for the JOI burn. It parks at 280Km. This is 1y 386d MET, meaning the intrepid kerbal crew waited in orbit for 113 days for LARS, even though their total mission time so far was a little under 2 days shorter than LARS’.

Rendezvous and Docking
As soon as LARS settled in its parking orbit, the LOLS crew starts working on the rendezvous maneuver. A good encounter happens after 5 orbits around Jool.


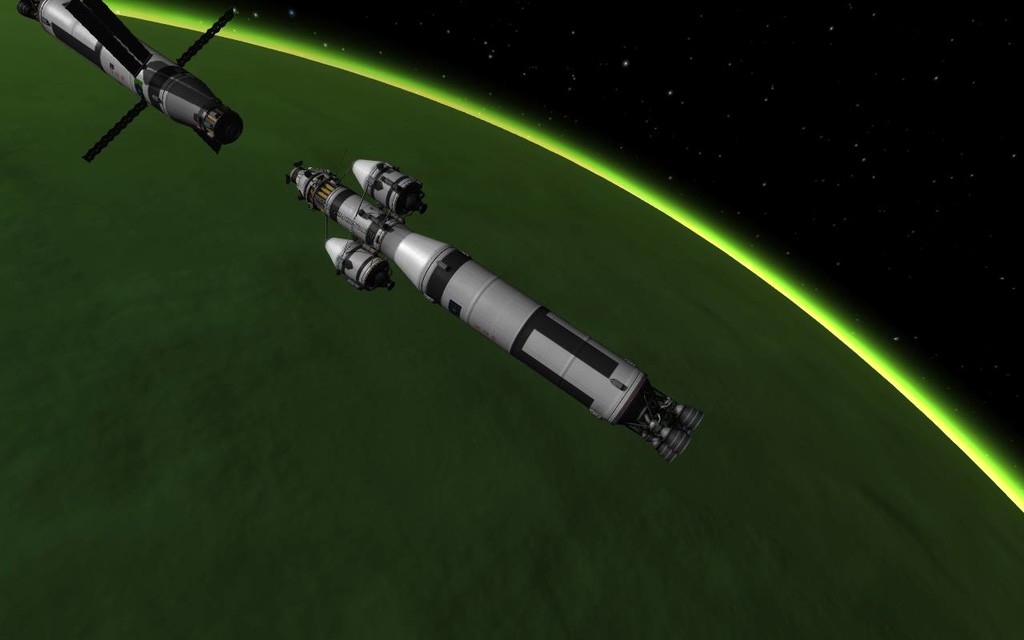
Once docked, the crew transfers all the fuel remaining on the LOLS main tank to LARS and ejects it. From now on, LARS will be doing the heavy lifting of the Trans-laythean Injection.
Trans-laythean Injection and Laythean Orbit Injection
(I mentioned early on that rendezvous in Jool orbit proved to be a mistake. The why might become more clear from this picture.)

The two small extra boosters added to LOLS made it a bit too much for the Clamp-O-Tron docking port to hold. When LARS ignited its engine for TLI, the centre of mass shifted slightly but enough to make LOLS wobble and put on too much stress on the docking port, which then broke. (Thankfully I had quicksaved just before the burn and was able to recover.)
The crew slowly pushes on the throttle to ease on the clamp-o-tron stress. Same thing during LOI: easy on the throttle. The crew and mission control also agreed to skip the aerobreaking, the rationale being that Laythe’s atmosphere is low (55Km) and not very dense so it would probably not help them all that much and they did not want to put on more stress on the docking port.

Undocking LOLS and Landing
At this point, the crew transfers fuel from the LARS main tank to the three LOLS tanks and undocked. Time to land.
Laythe is touch to land for two basic reasons:
- It’s almost entirely made of oceans, with some relatively small islands and continents; and also
- The islands and continents are rough! Lots of mountains and steep slopes.
The crew ultimately picked the continent that looks sort of like a large ‘C’ with an internal sea.

(It took me a few tries and one big scare as just before landing I noticed a deep valley just ahead.)

LMP Donbro Kerman uses the retro rockets plus the parachutes to slow the LOLS down and slowly descend.
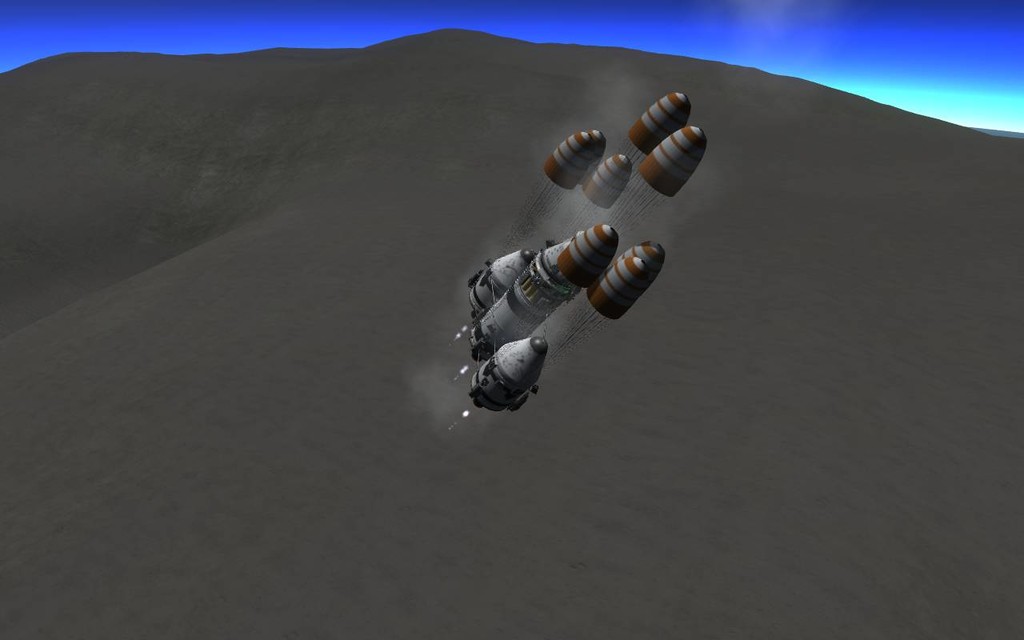
He also has to rotate LOLS around to make sure it lands in a way to prevent it from tumbling over the slope.
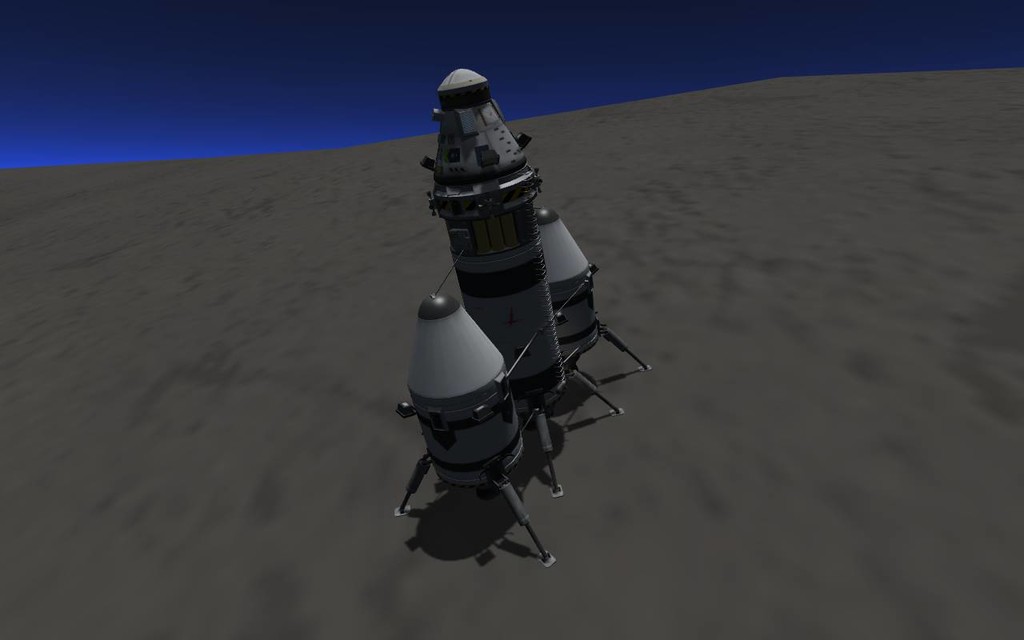
It all ends well though, as Commander Roley Kerman steps out of LOLS and steps on Laythe.
Laythe Base
The crew has to remain on the surface until the next interplanetary window before they could go back to Kerbin, which means: time for some science! With some gravioli detection, temperature and barometric measurements, EVA reports, crew reports, Mystery Goo™ observation, and some surface samples, the LOLS crew gets well over a thousand science points.
And they had some fun too, like this little night rave or whatever. This is Donbro standing by the lander legs while Tomner jumps by the flag.

Commander Roley was asleep and missed the shenanigans. Probably for the best.
Takeoff and rendezvous
After a couple of years on Laythe, the crew was eager to go back home.

LOLS rendezvous with LARS, which patiently waited all these years in orbit.



The crew now transfers the remaining fuel from the LOLS tank to LARS’ and jettisons it. Time to go home.
The jorney home
The jorney back is largely uneventful, starting with the transfer from Laythe back to Jool. Now that they got rid of the LOLS tanks, the Clamp-O-Tron docking port is more than capable of holding the capsule in place.
Back in orbit around Jool, LARS is GO for Trans-Kerbal Injection.

And the long journey back to Kerbin is now underway.
Two years later, the crew maneuvers to reach Kerbin with a periapsis of 30Km for some heavy aerobreaking.

They reemerge from Kerbal atmosphere with an apoapsis of almost 2,000Km and running of fumes. The remaining fuel is then used to lower the apoapsis a little bit without changing the periapsis too much. This made sure that on the second periapsis pass, the stack will not make it out of the atmosphere again.
At this point, mission control tries for a bonus mission objective. They plan to land both the LOLS capsule and the LARS rockets at the same time and try to recover the LARS hardware costs. After they stop burning in the reentry, the LOLS capsule undocks from LARS and mission control constantly switch between the two to try and land both.
Unfortunately, saving the LARS was a failure. As soon as the parachutes opened, LARS disintegrated, leaving only the RCS tank and docking port to slowly land.

The LOLS capsule on the other hand had a beautiful descent.

After LOLS splashed down, the capsule, its science payload, and its crew were successfuly recovered. Mission accomplished!

The remaining LARS parts were found to not be recoverable.

A few closing remarks
I was pretty pleased to have completed my longest mission yet. Still, a few things I would have changed.
I wasted fuel by not aerobreaking in Laythe. Also, I am sure there is an optimal altitude that I could have reached Jool for a better aerobreaking. I did try several but going even a bit under 105Km seemed to be too much as the ship never came back out of the atmosphere. A little over 110Km and the apoapsis would end up in the millions of kilometers.
Another thing is that I made the hop in Jool orbit between Kerbin and Laythe. I am not sure it is possible but I think I will try in the future to go directly to Laythe. It must be terribly difficult but a scenario would be to arrive in such an angle that you could aerobreak in Jool and come out with a path leading to Laythe directly, hopefully with some extra aerobreaking. This would be optimal but would require a lot of precision. I don’t think I could make it but it sure sounds like it would be fun.
I should also have scheduled the LOLS-LARS rendezvous to happen in orbit around Laythe instead of Jool to avoid the wobbly lander problem. The LOLS was low on fuel by that time though, so I am not really sure I could have pulled it off anyway.
And I could have taken at least one more Mystery Goo™ as I could have observed it in orbit aroud Laythe for some extra points.
And finally, I love this game so much. You learn more every time you play it. This whole thing, including designing both stacks and doing some testing, was done over the course of a few days, mostly last weekend with the return from Laythe to Jool and then Kerbin done over a couple of nights this week.
I thank Squad for this great game.
May your solar panels be always unobstructed.
UPDATE: this whole story was created way before KSP 1.0 came out. The aerobreaking maneuvers here would not have worked due to the lack of heat shields. As well, a scientist kerbal in the crew would solve my issue above with only taking a single Mystery Goo™ as kerbal scientists can reset experiments in flight.


![By Christopher Walker (Sadness) [CC BY-SA 2.0 (http://creativecommons.org/licenses/by-sa/2.0)], via Wikimedia Commons](https://robteix.com/wp-content/uploads/2014/10/1024px-Sadness_4-1024x678.jpg)








































